On Repeated Medical “testing”

I’ve blogged about this before, but I wanted to revisit because FiveThirtyEight, whom I love and adore, just posted about it again, in light of the recent Theranos problems.

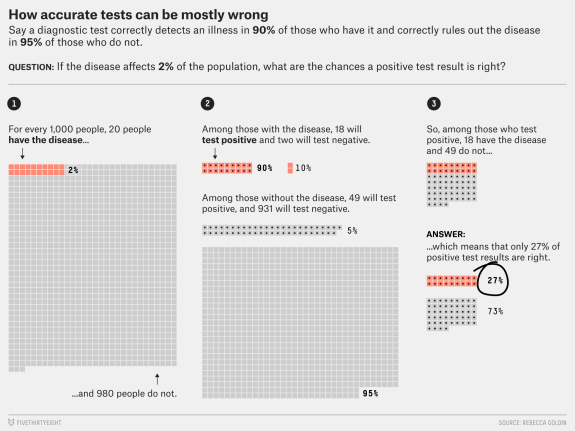
My last blog post was long, so let me simplify my position… there’s a big graphic in the middle of the FiveThirtyEight article:

And it’s fine, it’s very simple, very accurate math, EXCEPT, it only deals with the case where each person takes exactly one test.  This isn’t FiveThirtyEight’s fault, they borrowed a common example, and that example is what most medical research is based on… see the flow chart in my last post… you take blood, you look for things, and you (doctors and patients) react to what you find.

This is NOT the best way forward if cheap reapeatable tests become available.   It’s not: test, react, test, react, test, react – which I agree leads to over-reactive medicine.  It’s: test, test, test, react, which I’m arguing will reduce over-reaction (but I admit may not be for the feint of heart).

Here’s how the math works with the same numbers as above if we reduce test costs to 10% and spend the same amount in testing… that is, every person gets 10 tests for the same cost.

Important note… my probabilities, statistics, and combinatorics are rusty (thus the simulation at the end), but if these numbes are off, they’re not far off:

We have to assume those tests are independent — that is, something that triggers a false positive in one person isn’t some consistent genetic or chemical issue.  Anyway.

1. For every 1,000 people, 20 people have the disease (still).
2. Everyone will test positive between 0 and 10 times (because 10 tests each)
   1. Among those with the disease, the data looks more like a continum than binary (WHICH IS WHAT IT SHOULD LOOKE LIKE)…  what do I mean?
      1. Odds are pretty strong that an individual will have 7,8,9, or 10 positive results out of 10.  The odds of the first being a false negative are 1 in 10 (10% or 0.1).  The odds of the first two being negative are 0.1*0.1, three = 0.1*0.1*0.1, and so forth.  So the odds of someone with the disease having ten negative tests are astronomically low.  Low enough that in the twenty example people you should never really expect someone to have less than five positive results.
   2. Among those WITHOUT the disease, since the test is more precise, things are even better:
      1. Odds of a single false positive are 0.05, so the odds of 10 false positives for one person are ridiculous (0.05^10 = 9.77*10^-14, right?).   In a group of 1000 patients it will be surprising to see anyone with more than 4 false positives.
3. At this point, for me, it’s easier to simulate this than to do the math (my math degree is 20 years old after all).  And we can do that quickly in a spreadsheet or an R or python program.
   1. Make 1000 records, and label 20 with “1” (true positive) and the rest with 0 (true negative).
   2. Assign 10 random percentages to each record.
   3. For the 20 true positives, count the number of tests that are below 0.9
   4. For the 980 true negatives, count the number of tests that are above 0.95

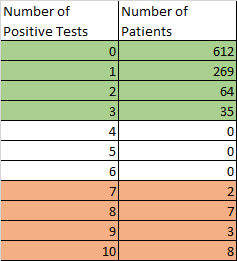
Here’s what I got:

Which doesn’t look so bad, does it?  The Green are the healthy patients, who all had less than 5 positive tests, and the strange coral color are the unhealthy patients, who all had more than 5 positive tests.  Yes, with large enough numbers of patients, 10 tests would start to see some anomalies bleed over, but compared to taking a single test and a single result, we’ve gone from a 27% result to a 100% result.  YES, it cost 10 times as much, in testing, but tests are way cheaper than treatment in most situations, and driving test costs down has a much stronger ROI, if we can get a three-ish-fold return in accuracy (27 to 100).

If doctors are complaining that the 368 patients who received at least one false positive are going to be an issue (269+64+35), then they need to be shown this chart and explained basic math.  The fact that we make bad medical decisions because people don’t understand the realities of medical tests is NOT a reason to turn down improvments in data collection.

ObFinalNote:  Theranos apparently has been, if not falsifying, at least misleading or misrepresenting the accuracy of its tests.  NO solution exists for tests that simply don’t work.  But given the thought experiment on the table, the math is in FAVOR of more testing, not less, if a) it becomes cost effective and b) we keep our heads about us.